Matrix Algebra

I. Vectors and Vector operations

We define two Column Vectors A and B

A is a 3 x 1 vector of scores from 3 subjects on an accuracy measure.

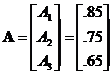
T is a 3 x 1 vector of scores from the same 3 subjects on response time.

---

1. Scalar Multiplication is obtained by multiplying each coordinate by a constant:

a = 2

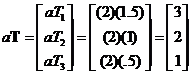
This operation expands or contracts the length of a vector. It can also reverse the direction if the scalar constant is negative.

---

2. Inner Product of two vectors produces a scalar:

A'T = A₁T₁ + A₂T₂ + A₃T₃

= (.85)(1.5) + (.75)(1.0) + (.65)(.50)

= 1.275 + .75 + .325 = 2.35

This is a measure of similarity between the two vectors.

If A'T = 0, then A and T are orthogonal vectors (right angles).

The angle q between the two vectors A and T can be determined from the law of cosines:

cos(q) = (A'T) / [Sqrt(A'A)Sqrt(T'T)]

---

3. Squared Length of a Vector:

A'A = A₁A₁ +A₂A₂ +A₃A₃

= (.85)(.85) +(75)(.75) +(.65)(.65)

= .7225 + .5625 + .4225 = 1.7075

If A'A = 1, then A is a normalized vector.

---

4. Sum of Two Vectors:

This is a new point obtained by starting at zero, traveling the full length of the first vector in the direction of the first vector, and then continuing from that point to travel the full length of the second vector in the direction of the second vector.

---

5. Difference Between Two Vectors:

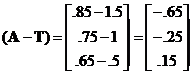
(A-T) gives the direction of the line connecting the two points.

Z = T + s(A-T) is a line containing A and T. If s = 0 then Z = T, if s = 1 then Z = A, if s = .5 then Z is halfway between T and A.

---

6. Squared Distance between Two Vectors:

(A-T)'(A-T) = (A₁-T₁)² + (A₂-T₂)² + (A₃-T₃)²

= (.85-1.5)² + (.75-1.0)² + (.65-.50)²

= .65² + .25² + .15² = .5075

---

II. Matrix Operations

Let X be defined as an example of a 3 x 2 matrix.

This means that it has n = 3 rows and p = 2 columns.

The three rows represent data from 3 subjects, labeled S₁, S₂, S₃.

The two columns represent measures on 2 different variables, A and T.

Matrix X	A = Accuracy	T = Response Time
S1'	.85	1.50
S2'	.75	1.00
S3'	.65	.50

X = [ A | T ]

=

x_jk = score in row j column k

x₂₁ = .75, x₁₂ = 1.50

Each row vector can be interpreted as a point in a 2 - dim space.

S₁' = [ .85 1.5]
S₂' = [.75 1.0]
S₃' = [.65 .50]

Plotting a point for each row produces a scatterplot

Each column A and T can be interpreted as a vector in a 3 - dim space.

---

1. Transpose operation applied to X changes rows into columns

X'	S1	S2	S3
A'	.85	.75	.65
T'	1.5	1.0	.50

---

2. Matrix product

Let b be an example of a column vector with two coefficients:

C = Xb produces a new column vector C.

Multiplying X (3 x 2) with b (2 x 1) produces C (3 x 1).

C can be computed two equivalent ways:

A. A linear combination of the column vectors.

C = Xb

= b₁A + b₂T

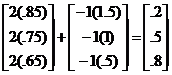
C = Xb is a point on a plane defined by X = [A | T ] that lies inside the 3 dimensional space.

b gives the coordinates on the plane defined by X that maps into the coordinates C = Xb that are defined in terms of the standard 3 -d space.

B. Column vector of inner products:

C = Xb =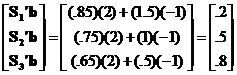

---

Now define a new 2 x 2 matrix

B=	b1	b2
B1'	2	.5
B2'	-1	.5

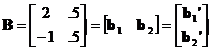
The product of X (3 x 2) with B (2 x 2) forms a new matrix C (3 x 2)

C = XB =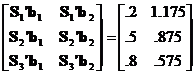

---

The product of BX does not exist. Inner dimensions must match.

Note: BX =/= XB

The product of B (2 x 2) with X' (2 x 3) is given by

---

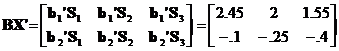
3. Outer Product:

The matrix product of a (3 x 1) column vector A with a (1 x 3) row vector T' forms an outer product

Another way to compute the product of a matrix is by the outer product

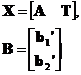
More Generally for n x m matrix X and m x p matrix B

---

4. Special Matrices

Square Matrix: This is a matrix that has the same number of rows as columns

e.g. X is n ´ n

Diagonal Matrix: This is a square matrix with non zero numbers only on the diagonal

e.g.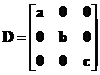

Identity matrix denoted I acts like the number one

X×I = X ,

This is a square matrix with ones on the diagonal and zeros everywhere else

e.g. for a 3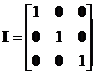

---

5. Matrix Inverse

Suppose we wish to solve for b in the equation y = x×b

the solution is

x^-1y = x^-1xb = 1b = b

Now suppose

X is a n ´ n matrix, and Y is a n ´ 1 column vector

Suppose we wish to solve for b in the equation

Y = Xb

We wish to find the inverse matrix of X, denoted X^-1 such that

X×X^-1 = I

Then we could solve for b by

X^-1Y = X^-1Xb = Ib = b

The matrix inverse of a diagonal matrix is the reciprocal of the diagonal elements.

e.g.

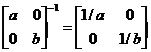
_{For a diagonal matrix ,}

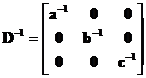
Here is the general formula for the inverse of a 2 x 2 matrix

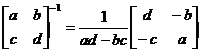
This can be check by

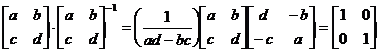
For larger matrices, the formula becomes too complicated.

Computers are used to compute this

Note: The inverse of a matrix does not always exist.

Requirements for an inverse to exist:

1. The matrix must be square

2. The columns (rows) must be linearly independent

no column is formed by a linear combination of the other columns

if this is violated then the matrix is singular or less than full rank

---

Transpose of product: (XB)’ = B’X’

Inverse of product: (XB)^{-1 =} B^-1X^-1 (assuming inverses exist)

---

Assume X is symmetric initially.

1. Spectral Decomposition of X:

X = VDV'

where V'V = I = VV' and D is diagonal.

V is a matrix of orthonormal column vectors.

Each column vector, V_j, is called an eigenvector (guaranteed to be real).

Each diagonal element of D, d_j, is an eigenvalue (also guaranteed to be real).

An equivalent way to write this decomposition is :

X = d₁V₁V₁' + d₂V₂V₂' + … + d_pV_pV_p'

Some Properties Related to Spectral Representation:

XV_j = d_jV_j

X² = VDV'VDV' = VD²V'

X^-1 = VD^-1V'

Finding Eigenvalues and Eigenvectors using determinants

Assume X is square and assume no repeated eigenvalues.

1. Spectral Decomposition of X:

X = VDV^-1

where V is full rankd and D is diagonal.

V is a matrix of linearly independent column vectors.

Each column vector, V_j, is called an eigenvector (could be complex).

Each diagonal element of D, d_j, is an eigenvalue (could be complex).

---

Example 2 x 2 matrix

X =

[p	q
q	r]

d₁ = {(p+r) - Sqrt[ (p+r)² -4(pr-qq) ] } / 2

d₂ = {(p+r) + Sqrt[ (p+r)² -4(pr-qq) ] } / 2

---

2. Matrix Determinant

Product of the Eigenvalues

Det(X) = d₁d₂…d_p

Some Properties of Determinants

Det(XY) = Det(X)Det(Y)

Det(X') = Det(X)

IF V is orthonormal then Det(V) = +1 or -1

Det(X^-1) = 1/Det(X)

---

3. Matrix Trace

Trace[X] = x₁₁ + x₂₂ + … + x_pp

= d₁ + d₂ + … + d_p

Product Rule for Traces

Trace(XY) = Trace(YX)

Click for Proofs of Some of the Properties in this Lecture

---

#S650 Time Series Analysis

#Basic Matrix Algebra Commands (Correspond to Matrix Algebra course notes)

#Written by Leslie M. Blaha, 3 September 2008

#Define column vectors A and T

A <- matrix(c(0.85,0.75,0.65),ncol=1)

T <- matrix(c(1.5,1,0.5),ncol=1)

#Scalar Multiplication

a <- 2

aT <- a*T

#Inner Product

A.T <- t(A)%*%T #Note that %*% is the command for matrix multiplication

#t(A) is the transpose of vector A

#Cosine of angle q between vectors A and T

cos.q <- (A.T)/(sqrt(t(A)%*%A)*sqrt(t(T)%*%T))

#Squared Length of Vector A

A.norm <- t(A)%*%A

#Sum and difference of two vectors

sum <- A+T

diff <- A-T

#Squared distance between vectors A and T

dist.square <- t(diff)%*%diff

#Define Matrix X=[A|T]

X <- cbind(A,T)

#reference the 2nd row of X

X[2,]

#reference the 1st column of X

X[,1]

#reference the jk-th entry, where row j=1, column k=2

X[1,2]

#Transpose the matrix

X.trans <- t(X)

#Matrix Product

b <- matrix(c(2,-1),ncol=1)

C <- X%*%b

B <- matrix(c(2,-1,0.5,0.5),ncol=2,byrow=FALSE)

C.2 <- X%*%B

C.3 <- B%*%t(X)

#Outer product

outer <- A%*%t(T)

#Create a Diagonal Matrix

D <- diag(c(1,2,3),nrow=3)

#Create an Identity Matrix, here 3x3

I <- diag(1,nrow=3)

#Matrix Inverse

Y <- matrix(c(1,1.1,0,1.1,2,0.1,0,0.1,3),byrow=TRUE,nrow=3,ncol=3)

Y.inverse <- solve(Y) #Note that only square matrices with linearly independent rows can be inverted

#Spectral Decomposition of Y (a symmetric 3x3 matrix), Y=UDV'

Y.svd <- svd(Y)

Y.svd$d #the diagonal entries of matrix D

Y.svd$u #the matrix U

Y.svd$v #the matrix V

#Matrix Determinant

Y.det <- det(Y)

#Matrix Trace

Y.trace <- sum(diag(Y))

#Eigenvalues and Eigenvectors

Y.eigen <- eigen(Y)

Y.eigen$values

Y.eigen$vectors