General Linear Model (Matrix Form)

1. Bivariate Regression Model Example

y _i = observed score on criterion for subject i

y _i* = predicted score on criterion for subject i

e_i = ( y_i – y_i^* ) = error score for subject i

X1_i = score on predictor variable X1 for subject i

X2_i = score on predictor variable X2 for subject i

Scalar form:

y₁^* = b₀ + b₁X1₁ + b₂X2₁

y₂^* = b₀ + b₁X1₂ + b₂X2₂

y₃^* = b₀ + b₁X1₃ + b₂X2₃

…

y_N^* = b₀ + b₁X1_N + b₂X2_N

Y = N x 1 column vector of criterion scores

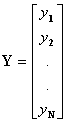
X = N x 3 matrix of predictor variable scores

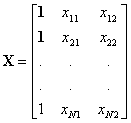
b = 3 x 1 column vector of regression coefficients

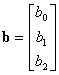
Matrix Form:

Y^* = Xb

E = (Y-Y^*)

II. General Estimation Problem: 

Y is N x 1, X is N x p, Y^* = Xb , E = Y-Y^*

Find b that minimizes SSE = E^'E (the squared length of E)

To solve this we need to find the projection Y^*=Xb of the point Y onto the plane X. The shortest distance is achieved when the difference E = (Y-Y^*) is orthogonal to the plane, i.e., X’E = X’(Y-Xb) = 0.

Proof: Suppose b satisfies (Y-Xb)’X = 0, and c satisfies (Y-Xc)’X =/= 0 

Define D = Xc – Xb so that Xc = Xb + D. Then

(Y-Xc)’(Y-Xc) = [Y – (Xb + D)]’[Y – (Xb + D)] = [(Y – Xb) – D]’[(Y - Xb) – D] 

= (Y-Xb)’(Y-Xb) – D’(Y-Xb) – (Y-Xb)’D + D’D = (Y-Xb)’(Y-Xb) + D’D > (Y-Xb)'(Y-Xb)

because D’(Y-Xb) = (c-b)’X’(Y-Xb) = 0 = (Y-Xb)’X(c-b) = (Y-Xb)’D . QED

Now that we have proved X’(Y-Xb) = 0 miminizes SSE

We can use this fact to solve for b : 

X’(Y-Xb) = 0 implies (X’Y) = (X’X)b so

General Solution: b = [(X’X)^-1X’]Y or b = PY, P = [(X’X)^-1X’]

III. General Linear Model (Univariate)

Y = Xb + e

X is the fixed design matrix

b is the population regression coefficient vector 

e ~ Normal ( 0 , s ²I ) implies Y~ Normal ( Xb , s ²I )

Some Properties of Least Squares Estimates: 

b = [(X'X)^-1X']Y = PY

E [ b ] = E { PY } = E{(X'X)^-1X'(Xb + e)}= E[ b + e ] = b .

Cov(b,b) = Cov( PY, PY) = PCov(Y,Y)P' = s ²PP' = s ²(X'X)^-1 .

IV. General Linear Model (Multivariate)

Y = N x p matrix of scores from N subjects on p criterion variables

X = N x q matrix of scores from N subjects on q predictor variables

B = (X'X)^-1(X'Y) = q x p matrix of regression coefficients

Y^* = XB = N x p matrix of predictions

E = Y - Y^* matrix of residuals 

Hypothesis Testing:

C = (g x q) pre contrast matrix (between subjects contrasts)

A = (p x u) post contrast matrix (within subjects contrasts)

D = CBA = (g x u) contrast matrix

H0: E [ D ] = 0

Q_e = A'[ E'E ]A

Q_h = D'[ C(X'X)^-1C' ]^-1D

L = Det(Q_e) / Det(Q_e + Q_h) ,

L ~ Wilks Lambda with df = (u,g,N-q)

F = [ (1 - L ^1/t ) / L ^1/t ][ df_D / df_N ]

df_N = (g)(u)

df_D = (r)(t)-2w

r = (N-q)-(u-g+1)/2

w = ( gu -2)/4

t = Sqrt[ (g²u² - 4)/(g² + u² - 5)] if (g²+u² - 5) > 0, t = 1 otherwise.

Model Comparison View of Qh

Assume A = I

Define:

Y* = XB   (predictions from complete model)

Y_R* = XB_R ( B_R is restricted to satisfy the constraints imposed by E[CB] = 0 )

Then

Qh = [ (Y*)'(Y*) - (Y_R*)'(Y_R*) ] = (CB)'[C(X'X)^-1C']^-1(CB)

SAS and Matlab Programs

Example Repeated Measures ANOVA MATLAb Program

Example Specific Contrast