108 Dynamic Decision Making

Jerome R. Busemeyer

Indiana University

November 5, 1999

To appear in

International Encyclopedia of the Social and Behavioral Sciences: Methodology. Mathematics and Computer science. Amsterdam: Pergamon.

Jerome R. Busemeyer

Psychology Department

Indiana University

Bloomington, In 47405

Phone: 812-855-4882

email: jbusemey@indiana.edu

Contract No. 20851A2/2/051

Abstract

This section reviews a specialty within the field of decision-making known as dynamic decision-making. Dynamic decisions are characterized by a decision-maker choosing among various actions at different points in time in order to control and optimize performance of a dynamic stochastic system. Realistic examples include fighting fires, navigational control, battlefield decisions, medical emergencies, and so on. The section has four parts: The first reviews basic theory concerning optimal decision principles in a dynamic context; the second summarizes empirical approaches to the study of human performance on dynamic decision tasks; the third presents theoretical models that describe how humans learn to control dynamic systems; and the last discusses methodological issues arising from the study of complex decisions including differences between field versus laboratory research.

108 Dynamic Decision Making

Dynamic decision making is defined by three common features: A series of actions must be taken over time to achieve some overall goal; the actions are interdependent so that later decisions depend on earlier actions; and the environment changes both spontaneously and as a consequence of earlier actions (Edwards, 1962). Dynamic decision tasks differ from sequential decision tasks (see Diederich, in press) in that the former are primarily concerned with controlling dynamic systems over time, whereas the latter are more concerned with sequential search for information used to be use in making decisions.

Psychological research on dynamic decision making began with Toda's (1962) pioneering study of human performance on a game called the "fungus eater," in which human subjects controlled a robot's search for uranium and fuel on a hypothetical planet. Subsequently, human performance has been examined across a wide variety of dynamic decision tasks including computer games designed to simulate stock purchases (Ebert, 1972; Rapoport, 1966), welfare management (Dorner, 1980; Mackinnon & Wearing, 1980), vehicle navigation (Jagacinski & Miller, 1978; Anzai, 1984), health management (Kleinmuntz &Thomas, 1987; Kerstholt, 1994), production and inventory control (Sterman, 1989; Berry & Broadbent, 1988), supervisory control (Kirlik, Plamondon, Lytton, & Jagacinski, 1993), and fire-fighting (Brehmer & Allard, 1991). Cumulative progress in this field has been summarized in a series of empirical reviews by Edwards (1962), Rapoport (1975), Funke (1991), Brehmer (1992), Sterman (1994), Kerstholt and Raaijmakers (1997).

1. Stochastic Optimal Control Theory

To illustrate how psychologists study human performance on dynamic decision tasks, consider the following experiment by You (1989). Subjects were initially presented a "cover" story describing the task: "Imagine that you are being trained as a psychiatrist, and your job is to treat patients using a psychoactive drug to maintain their health at some ideal level." Subjects were instructed to choose the drug level for each day of a simulated patient after viewing all of a patient's previous records (treatments and health states). Subjects were trained on 20 simulated patients, with 14 days per patient, all controlled by a computer simulation program.

There are a few general points to make about this type of task. First, laboratory tasks such as this are oversimplifications of real life tasks, designed for experimental control and theoretical tractability. However, more complex simulations also have been studied to provide greater realism (e.g., Brehmer & Allard's, 1991, fire-fighting task). Second, the above task is an example of a discrete time task (only the sequence of events is important), but real time simulations have also been examined where the timing of decisions becomes critical (e.g., Brehmer & Allard's, 1991, fire-fighting task). Third, the cover story (e.g., health management) provides important prior knowledge for solving the task, and so the findings depend both on the abstract task properties as well as the concrete task details (Kleiter, 1975). Fourth, the stimulus events are no longer under complete control of the experimenter, but instead they are also influenced by the subject's own behavior. Thus experimenters need to switch from a stimulus - response toward a cybernetic paradigm for designing research (cf. Brehmer, 1992; Rapoport, 1975).

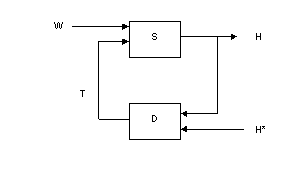
This health management task can be formalized by defining H(t) as the state of the patient's health on day t ; T(t) is the drug treatment presented on day t; and w(t) is a random shock that may disturb the patient on any given day. Figure 1 is a feedback diagram that illustrates this dynamic decision task. In this figure, S represents the environmental system that takes both the disturbance, w, and the decision maker's control action, T, as inputs, and produces the patient's state of health, H, as output. D represents the decision-maker's policy that takes both the observed, H, and desired, H*, states of health as input, and produces the control action, T, as output.

Based on these definitions, this task can be analyzed as a stochastic linear optimal control problem (Rouse, 1980): Determine treatments T(1), …, T(N), for N = 14 days, that minimize the objective function

F = E { S _t=1,N a [ H(t)-H*(t) ]² + b T²(t) }, (1)

contingent upon the linear stochastic dynamic system,

H(t+1) = a₁H(t) + a₂H(t-1) + b₁T(t) + b₂T(t-1) + b₃T(t-2) + w(t). (2)

Standard dynamic programming methods (Bertsekas, 1976) may be used to find the optimal solution to this problem. For the special case where the desired state of health is neutral (H* = 0), some treatment effect takes place the very next day (b₁ is nonzero), and there is no cost associated with the treatments (i.e., b = 0), then the optimal policy

T(t) = -[(a₁ / b₁)H(t) +(a₂ / b₁)H(t-1) + (b₂ / b₁)T(t-1) + (b₃ / b₁)T(t-2)] (3)

is the treatment that forces the mean health state to equal the ideal (zero) on the next day. If the cost of treatment is nonzero (i.e., b > 0), then the solution is a more complex linear function of the previous health states and past treatments (see Bertsekas, 1976; You, 1989).

Dynamic programming is a general-purpose method that can be used to solve for optimal solutions to many dynamic decision tasks. Although the example above employed a linear control task, dynamic programming can also been used to solve many nonlinear control problems (see Bertsekas, 1976). However, for highly complex tasks, dynamic programming may not be practical, and heuristic search methods such as genetic algorithms (Holland, 1994) may be more useful.

The formal task analysis presented above provides a basis for determining factors that may affect human performance on the task (cf., Brehmer, 1992). One factor is the stability of the dynamic system, which for Equation 2 depends on the two coefficients, a₁ and a₂. In particular, this system is stable if the roots of the characteristic equation,

l² -a₁l -a₂ = 0,

are less than one in magnitude (see Luenberger, 1979). A second factor is the controllability of the system, which depends on the three coefficients, b₁ b₂ and b₃ (see Luenberger, 1979). For example, if the treatment effect is delayed (b₁ = 0), then the simple control policy shown in Equation 3 is no longer feasible, and the optimal policy is more a complex linear function of the system coefficients.

Consistent with previous research, You (1989) found that even after extensive experience with the task, subjects frequently lost control of their patients and the average performance of human subjects fell far below optimal performance. But this is a gross understatement. Sterman (1989) found that when subjects tried to manage a simulated production task, they produced costs 10 times greater than optimal, and their decisions induced costly cycles even though the consumer demand was constant. Brehmer & Allard (1991) found that when subjects tried to fight simulated forest fires, they frequently allowed their headquarters to burn down despite desperate efforts to put the fire out. Kleinmuntz & Thomas (1987) found that when subjects tried to manage their simulated patients' health, they often let their patients die while wasting time waiting for the results of non-diagnostic tests and performed more poorly than a random benchmark.

2. Alternative Explanations for Human Performance

There are many alternative reasons for this sub-optimal performance. By their very nature, dynamic decision tasks entail the coordination of many tightly interrelated psychological processes including causal learning, planning, problem solving, and decision-making (cf. Toda, 1962). Six different psychological approaches for understanding human dynamic decision-making behavior have been proposed, each focusing on one of the component processes.

The first approach was proposed by Rapoport (1975), who suggested that sub-optimal performance could be derived from an optimal model either by adding information processing constraints on the planning process, or by including subjective utilities into the objective function of Equation 1. For example, Rapoport (1966; 1967) found that human performance in his stock purchasing tasks was accurately reproduced by assuming that subjects could only plan a few steps ahead (about 3 steps), as compared to the optimal model with an unlimited planning horizon. In this case, dynamic programming was useful for providing insights about the constraints on human planning capabilities. As another example, Rapoport, Jones, & Kahan (1970) attempted to predict performance in a multi-stage investment game by assuming that the utility function was a concave function of monetary value. In this case, Rapoport et al. (1970) used dynamic programming to derive an elegant decision rule, which predicted that investments should be independent of the size of the capital accumulated during play. Contrary to this prediction, human decision-makers were strongly influenced by this factor, and so in this case, dynamic programming was useful for revealing empirical flaws with the theory.

An alternative approach, proposed by Brehmer (1992) and Sterman (1994), is that sub-optimal performance is caused by a misconception of the dynamic system (Equation 2). In other words, a subject's internal model of the system does not match the true model. In particular, human performers seem to have great discerning the influence of delayed feedback and understanding the effects of nonlinear terms in the system. Essentially, subjects solve the problem as if it was a linear system that has only zero lag terms. In the case of Equation 2, the subjective decision policy is simply:

T(t) = -c₁ H(t),

where c₁ is estimated from a subject's control decisions. Sterman (1989) and Diehl & Sterman (1993) found that this type of simplified subjective policy described their subjects' behavior very accurately.

A more general method for estimating subjective decision policies was proposed by Jagacinski (Jagacinski & Miller, 1978; Jagacinski & Hah, 1988). Consider once again the example problem employed by You (1989). In this case, a subject's treatment decision on each trial T(t) could be represented by a linear control model:

T(t) = c₀ + c₁H(t) + c₂H(t-1) + c₃H(t-2) + c₄T(t) + c₅T(t-1) + c₆T(t-2) + error,

where the subjective coefficients (c₀, c₁, …, c₆) are estimated by a multiple regression analysis. This is virtually the same as performing a "lens model" analysis to reveal the decision-maker's policy (see Kleinmuntz, 1973; Slovic & Lichtenstein, 1972). This approach has been successfully applied in numerous applications (Jagacinski & Miller, 1978; Jagacinski & Hall, 1988; Kerlik, Miller, Jagacinski, 1993; Kleinman, Pattipati, & Ephrath, 1980; You, 1989). Indeed, You (1989) found that subjects made use of both lags 1 and 2 for making their treatment decisions.

Heuristic approaches to strategy selection in dynamic decision tasks have been explored by Kleinmuntz (1985; Kleinmuntz & Thomas, 1987) and Kerstholt (1994; 1996). These researchers examined health management tasks that entailed dividing time between two strategies: collecting information from diagnostic tests before choosing a treatment, versus treating patients immediately without conducting any more diagnostic tests. A general finding is that even experienced subjects tend to overuse information collection, resulting in poorer performance than that which could be obtained from a pure treatment (no test) strategy. This finding seems to run counter to the adaptive decision making hypothesis of Payne, Bettman, & Johnson (1993), which claims that subjects prefer to minimize effort and maximize performance. The information collection strategy is both more effortful and less effective than the treatment strategy in this situation.

Finally, an individual difference approach to understanding performance on complex dynamic decision tasks was developed by Dorner and his colleagues (see Funke, 1991, for a review). Subjects are divided into two groups (good versus poor) on the basis of their performance on a complex dynamic decision task. Subsequently, these groups are compared on various behaviors to identify the critical determinants of performance. This research indicates that subjects who perform best are those that set integrative goals, collect systematic information, and evaluate progress toward these goals. Subjects who tend to shift from one specific goal to another, or focus exclusively on only one specific goal, perform more poorly.

3. Learning to Control Dynamic Systems.

Although human performers remain sub-optimal even after extensive task training, almost all past studies reveal systematic learning effects. First, overall performance rapidly improves with training (see e.g., Brehmer, 1992; Sterman, 1989; Mackinnon & Wearing, 1985; Rapoport, 1966). Furthermore, subjective policies tend to evolve over trial blocks toward the optimal policy (Jagacinski & Miller, 1978; Jagacinski & Ha, 1988; You, 1989). Therefore, learning processes are important for explaining much of the variance in human performance on dynamic decision tasks (cf., Hogarth, 1981). Three different frameworks for modeling human learning processes in dynamic decision tasks have been proposed.

A production rule model was developed by Anzai (1984) to describe how humans learn to navigate a simulated ship. The general idea is that past and current states of the problem are stored in working memory. Rules for transformation of the physical and mental states are represented as condition-action type production rules. A product rule fires whenever the current state of working memory matches the conditions for a rule. When a production rule fires, it deposits new inferences or information in memory, and it may also produce physical changes in the state of the system. Navigation is achieved by a series of such recognize -act cycles of the production system. Learning occurs by creating new production rules that prevent earlier erroneous actions, and new rules are formed on the basis of means - ends type of analyses for generating sub-goal strategies. Simulation results indicated that the model learned strategies similar to those produced in the verbal protocols of subjects, although evaluation of the model was dependant on qualitative judgments rather than quantitative measurements.

An instance or exemplar based model was later developed by Dienes and Fahey (1995) to describe how humans learn to control a simulated sugar production task, and to describe how they learn to manage the emotional state of a hypothetical person. This model assumes that whenever an action leads to a successful outcome, then the preceding situation and the successful response are stored together in memory. On any given trial, stored instances are retrieved on the basis of similarity to the current situation, and the associated response is applied to the current situation. This model was compared to a simple rule-based model like that employed by Anzai (1984). The results indicated that the exemplar learning model produced more accurate predictions for delayed feedback systems, but the rule based model performed better when no feedback delays were involved. This conclusion agrees with earlier ideas presented by Berry and Broadbent (1988) that delayed feedback tasks involve implicit learning process, whereas tasks without delay are based on explicit learning processes.

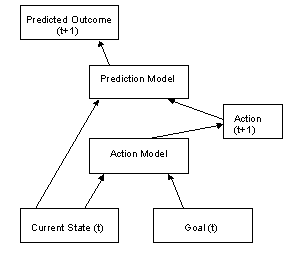
An artificial neural network model was recently developed by Gibson, Fichman, & Plaut (1998) to describe learning in a sugar production task. Figure 2 illustrates the basic idea.

At the bottom of the figure are two types of input nodes, one representing the current state of the environment, and the other representing the current goal for the task. These inputs feed into the next layer of hidden nodes that compute the next action given the current state and goal. The action and the current state then feed into another layer of hidden nodes, which is used to predict the consequence of the action given the current state. The connections from the current state and action to the prediction hidden layer are learned by back propagating prediction errors; and the connections from the current state and current goal to the action hidden layer are learned by back propagating deviations between the observed outcome and the goal state (holding the connections to the prediction layer constant, see Jordan & Rumelhart, 1992, for more details). This learning model provided good accounts of subjects’ performance during both training and subsequent generalization tests under novel conditions. Unfortunately, no direct comparisons with rule or exemplar based learning models were conducted, and this remains a challenge for future research.

Another type of neural network model for learning dynamic systems is the reinforcement learning model (see Sutton & Barto, 1998, for a review of this approach). Although this approach has proven to be quite successful for robotic applications (see Miller, Sutton, & Werbos, 1991), it has not yet been empirically tested against human performance in dynamic decision tasks.

4. Laboratory versus Naturalistic Decision Research

Klein and his associates (Klein, Orasanu, Calderwood, & Zsambok, 1993; Zsambok & Klein, 1997) have made progress toward understanding dynamic decisions in applied field research settings, which they call naturalistic decision making (e.g., interview fire chiefs after fighting a fire). Field research complements laboratory research in two ways: On the one hand, it provides a reality check on the practical importance of theory developed in the laboratory; on the other hand, it provides new insights that can be tested with more control in the laboratory.

The general findings drawn from naturalistic decision research provide converging support for the general theoretical conclusions obtained from the laboratory. First, it is somewhat of a misnomer to label this kind of research “decision-making,” because decision processes comprise only one of the many cognitive processes engaged by these tasks -- learning, planning, and problem – solving are just as important. Decision-making is used to define the overall goal, but then the sequence of actions follows a plan that has either been learned in the past or generated by a problem – solving process. Second, learning processes may explain much of the variance in human performance on dynamic decision tasks. Decision-makers use the current goal and current state of the environment to retrieve actions that have worked under similar circumstances in the past. Klein's (1998) recognition-primed decision model is based on this principle, and this same basic idea underlies the production rule, exemplar, and neural network learning models. Third, learning from extensive experience is the key to understanding why novel subjects fail where experts succeed. A few hundred trials in a laboratory task are relatively insignificant in comparison with say 25 years of experience on a job. Naïve subjects may fail to prevent their headquarters from burning down in a simulated forest fire, but expert fire-chiefs succeed in saving our national parks from forest fires every year.

References

Anzai, Y. (1984) Cognitive control of real -time event driven systems. Cognitive Science,

8, 221-254.

Berry, D. C. & Broadbent, D. E. (1988) Interactive tasks and the implicit-explicit

distinction. British Journal of Psychology, 79, 251-272.

Bertsekas, D. P. (1976) Dynamic programming and stochastic control.

N.Y. Academic Press.

Brehmer, B. (1992) Dynamic decsion making: Human control of complex systems.

Acta Psychologica, 81, 211-241.

Brehmer, B. & Allard, R. (1991) Real-time dynamic decision making: Effects of task

complexity and feedback delays. In J. Rasmussen, B. Brehmer, and J. Leplat

(Eds.) Distributed decision making; Cognitive models for cooperative work.

Chichester: Wiley.

Diederich, A. (in press) Sequential decision making. In Marley, T. (Ed.) Intenational

Encyclopedia of the Social and Behavioral Sciences: Methodology. Mathematics

and computer science. Amsterdam: Pergamon.

Diehl, E. & Sterman, J. D. (1993) Effects of feedback complexity on dynamic decision

making. Organizational Behavior and Human Decision Processes, 62, 198-215.

Dienes, Z. & Fahey, R. (1995) Role of specific instances in controlling a dynamic

system. Journal of Experimental Psychology: Learning, Memory, & Cognition,

21, 848-862.

Dorner, D. (1980)On the problems people have in dealing with complexity. Simulation

and Games, 11, 87-106.

Ebert, R. J. (1972) Human control of a two-variable decision system. Organizational

Behavior and Human Performance, 7, 237-264.

Edwards, W. (1962) Dynamic decision theory and probabilistic information processing.

Human Factors, 4, 59-73.

Funke, J. (1991) Solving complex problems: Exploration and control of complex

systems. In R. J. Sternberg and P. A. Frensch (Eds.) Complex problem solving:

Principles and mechanisms. Hillside, N.J.: Erlbaum.

Gibson, F., Fichman, M. & Plaut, D. C. (1997) Learning in dynamic decision tasks:

Computational model and empirical evidence. Organizational Behavior

and Human Performance, 71, 1-35.

Hogarth, R. M. (1981) Beyond discrete biases: Functional and dysfunctional aspects

of judgmental heuristics. Psychological Bulletin, 90, 197-217.

Holland, J. (1994) Adaptation in natural and artificial systems. Cambridge: MIT Press.

Jagacinski, R. J. & Miller, R. A. (1978) Describing the human operator's internal model

of a dynamic system. Human Factors, 20, 425-433.

Jagacinski, R. J. & Hah, S. (1988) Progression-regression effects in tracking repeated

patterns. Journal of Experimental Psychology: Human Perception and

Performance, 14, 77-88.

Jordan, M. I. & Rumelhart, D. E. (1992) Forward models: Supervised learning with a

distal teacher. Cognitive Science, 16, 307-354.

Kerstholt, J. H. (1994) The effect of time pressure on decision making behavior in a

dynamic task environment. Acta Psychologica, 86, 89-104.

Kerstholt, J. H. (1996) The effects of information costs on strategy selection in

dynamic tasks. Acta Psychologica, 94, 273-290.

Kerstholt, J. H., & Raaijmakers, J. G. W. (1997) Decision making in dynamic task

environments. In W. R. Crozier & O. Svenson (Eds.) Decision making:

Cognitive models and explanations. London: Routledge. (Pp. 205-217).

Kirlik, A., Miller, R. A., & Jagacinski, R. J. (1993) Supervisory control in a dynamic and

uncertain environment: A process model of skilled human-environment

interaction. IEEE Transactions on Systems, Man, and Cybernetics, 23,

929-952.

Kirlik, A. Plamondon, D. D., Lytton, L. & Jagacinski, R. J. (1993) Supervisory control

in a dynamic and uncertain environment: Laboratory task and crew performance.

IEEE Transactions on Systems, Man, and Cybernetics, 23, 1130-1138.

Klein, G. (1998) Sources of Power: How people make decisions. Cambridge: MIT Press.

Klein, G., Orasanu, J., Calderwood, R., & Zsambok, C. E. (1993) Decision making in

action: Models and methods. Norwood, NJ: Ablex.

Kleinman, D. L., Pattipati, K. R., & Ephrath, A. R. (1980) Quantifying an internal model

of target motion in a manual tracking task. IEEE Transactions on Systems, Man,

and Cybernetics, 10, 624-636.

Kleinmuntz, D. (1985) Cognitive heuristics and feedback in a dynamic decision

environment. Management Science, 31, 680-702.

Kleinmuntz, D. (1993) Information processing and misperceptions of the implications of feedback

in dynamic decision making. System-Dynamics-Review, 9, 223-237.

Kleinmuntz, D. & Thomas, J. (1987) The value of action and inference in dynamic

decision making. Organizational Behavior and Human Decision Processes, 39,

341-364.

Kleiter, G. D. (1975) Dynamic decision behavior: Comments on Rapoport's paper.

In D. Wendt & C. Vlek (Eds.) Utility, Probability, and Human Decision Making,

Dordrecht-Holland: Reidel. (Pp. 371-380).

Luenberger, D. G. (1979) Introduction to dynamic systems. N.Y.: Wiley.

Mackinnon, A. J. & Wearing, A. J. (1980) Complexity and decision making.

Behavioral Science, 25, 285-296.

Mackinnon, A. J., & Wearing, A. J. (1985) Systems analysis and dynamic decision

making. Acta Psychologica, 58, 159-172.

Miller, W. T., Sutton, R. S., & Werbos, P. J. (1991) Neural networks for control.

Cambridge, MA: MIT press.

Payne, J. W., Bettman, J. R., & Johnson, E. J. (1993) The adaptive decision maker.

NY: Cambridge University Press.

Rapoport, A. (1966) A study of human control in a stochastic multistage decision task.

Behavioral Science, 11, 18-32.

Rapoport, A. (1967) Dynamic programming models for multistage decision making.

Journal of Mathematical Psychology, 4, 48-71.

Rapoport, A. (1975) Research paradigms for studying dynamic decision behavior.

In D. Wendt & C. Vlek (Eds.) Utility, Probability, and Human Decision Making,

Dordrecht-Holland: Reidel. (Pp. 347-369).

Rapoport, A., Jones, L. V., & Kahan, J. P. (1970) Gambling behavior in multiple-choice

Multi-stage betting games. Journal of Mathematical Psychology, 7, 12-36.

Rouse, W. B. (1980) Systems engineering models of human-machine interaction.

N.Y.: North-Holland.

Slovic. P. & Lichtenstein, S.(1971) Comparison of Bayesian and regression approaches

to the study of information processing in judgment. Organizational Behavior

and Human Peformance, 6, 649-744.

Sterman, J. D. (1989) Misperceptions of feedback in dynamic decision making.

Organizational Behavior and Human Decision Processes, 43, 301-335.

Sterman, J. D. (1994) Learning in and about complex systems. System Dynamics

Review, 10, 291-330.

Sutton, R. S. & Barto, A. G.(1998) Reinforcement learning. Cambridge, MA: MIT press.

Toda, M.(1962) The design of the fungus eater: A model of human behavior in an

unsophisticated environment. Behavioral Science, 7, 164-183.

You (1989) Disclosing the decision - maker's internal model and control policy in a

dynamic decision task using a system control paradigm. Unpublished MA thesis,

Purdue University.

Zsambok, C. E. & Klein, G. (1997) Naturalistic decision making. Mahwah, NJ:Erlbaum.